人肉计算(7): 社会行为分析

在上一篇文章中我们讨论了预测市场在某种意义上也是在聚合人类的输入。到目前为止我们已经看过足够多的金融领域在人肉计算中将人类输入进行聚合的例子。这次我们来看一看社会行为分析领域中的三个相关的技术和问题：

基于代理人的建模与模拟
随机模型
社会同步性

社会行为分析旨在探索人口规模下的用户行为的模型的结果。

基于代理人的建模与模拟

首先，一个基于代理人的模型 (Agent-Based Model, ABM, Individual-Based Model, 基于个人的模型) 的模拟系统指定了一系列的代理人（agent）。

定义：一个代理人是一个实体，它模拟了个人、团体或组织，具有一个行为，并与其他代理人互动或影响，同事根据规则、可能、随机性来自主决定其行为。

ABM 可以指定不同类型的代理人。ABM 模拟了大量代理人的同步动作或大量代理人之间的交互，从而模拟现实生活系统（如生物生态系统，交通网络或市场）以及预测现实生活中现象的出现。

值得一提的是，ABM 的关键问题在于从微观层面行为 (micro-level behaviors) 暴露出来的（如驱动因素或投资者的决策）宏观层面的现象 (macro-level phenomena)，如交通堵塞或市场泡沫或秩序 (order)，比如在可持续生态系统中等。这些内容并不会被明确地建模或编制到 ABM 中去。

因此，ABM 其实是基于这个直觉假设的：简单的个人行为可能会产生一个更复杂的行为，即「整体超过其部分的总和」。

代理人通常在以下情况下被模拟：

当处于不同「粒度」时，即模拟各种规模的个人或组织的现实生活中；
当作为合理性时；
当知识普遍局部有限时；
当依靠简单的决策规则或是启发式时；
当以目标为导向时；
当作为以下几种能力时：
- 适应不断变化的情况（代理人一般有一个状态）；
- 学习；
- 繁殖（生物学）；
- 受其他代理人的影响；
- 与其他代理人互动；
- 与与其他代理人共享的环境相互作用；当然，也可能以多种各种方式组合。

ABM 通常包括：

多种多样的代理人；
代理人之间进行交互的拓扑关系，比如进化邻居图（evolving neighborhood graph）中的代理人可能会在其中移动；
代理人共享的、非代理人的、不断发展的环境；

ABM 也可以看作是一种补充分析方法：

分析方法可用于具有分析表征的系统现象；
ABM 可以模拟没有分析特征的系统的现象；

ABM 已经有大量的基于代理的建模工具：

编程语言中的程序库，如
- C++，
- Java（如 A3 或 AAA 或 Agent Anytime Anywhere），
- Prolog（如 DigiHive ）;
特定语言（如 ABLE，Agent Building 和 Learning ENvironment 以及 Brahms）
完全不需要编程的接口（如 Altreva Adaptive Modeler）。

关于 ABM 的更多论述可以参考文献 ¹, ², ³。

随机模型

随机模型（stochastic model）由有限的状态以及这些状态之间的转移概率组成。

简单随机模型服从马尔可夫性（Markov property）或是无记忆性（memoryless），即状态转换仅取决于当前状态（可能来自模型外部的输入）。假设模型具备马尔可夫性便能产生易处理随机模型。但当不具备马尔可夫性时，随机模型通常很棘手。

一个马尔可夫模型由一个状态转移图描述。对于一个门的状态转移图可以有两个状态：打开、关闭。

随机模型能够被用于在社会媒体或者游戏中分析社会行为：

基于人类可以在社交媒体上进行的动作或玩游戏来构建随机模型；
将模型的预测与观察到的人类行为进行比较；
修改社交媒体或游戏，以更好地反映观察到的行为；
重复该过程，直到模型充分反映观察到的行为。

下面我们来介绍一下基于社交新闻聚合器 Digg 的随机模型的分析。

在 Digg 中，用户可以提交新闻报道，并把他们通过「赞同」或「反对」来评价新闻报道。Digg 的每日头版由用户协作创建：

每天约有16,000个故事由用户提交
其中100人通过用户的投票晋升到首页

Digg 用户是否给他们注意到的新闻点赞，取决于他们的 Digg 朋友-粉丝关系：

Digg的朋友-粉丝关系是不对称的：爱丽丝→鲍勃
- Alice 是 Bob 的朋友
- Bob 是 Alice 的粉丝
一个新提交的文章是可见的
- 对提交者的粉丝来说是如此
- 对于所有来自「即将到来的文章列表」也是如此
点赞的文章对于点赞者的粉丝来说是可见的

给出一个提交的故事，一个不是提交者的粉丝和选民的粉丝的Digg用户被称为非粉丝。

状态转换图表示了一个用户的行为：

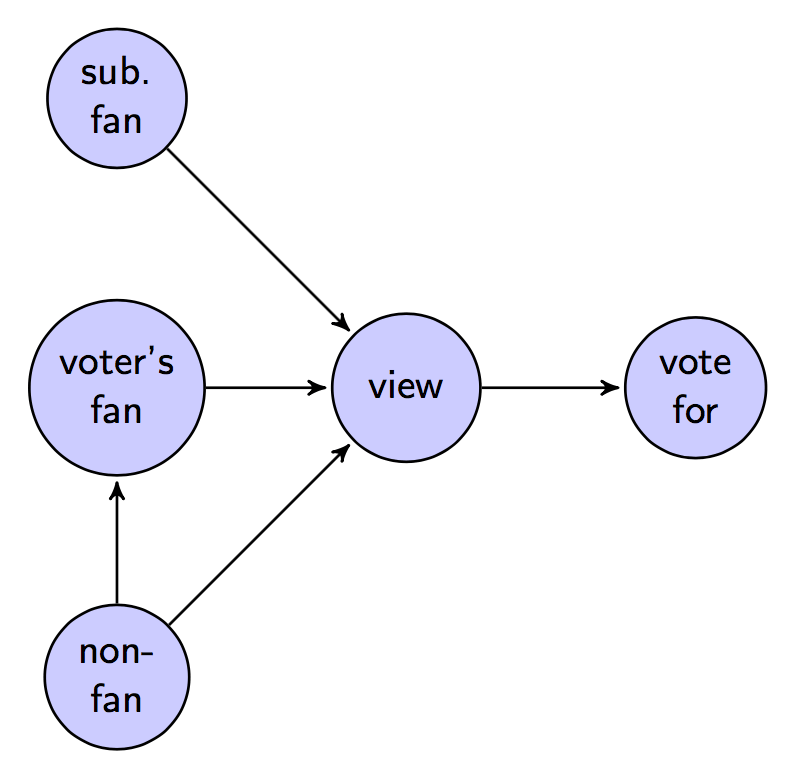
在 Digg 上表示文章命运的状态转换图：

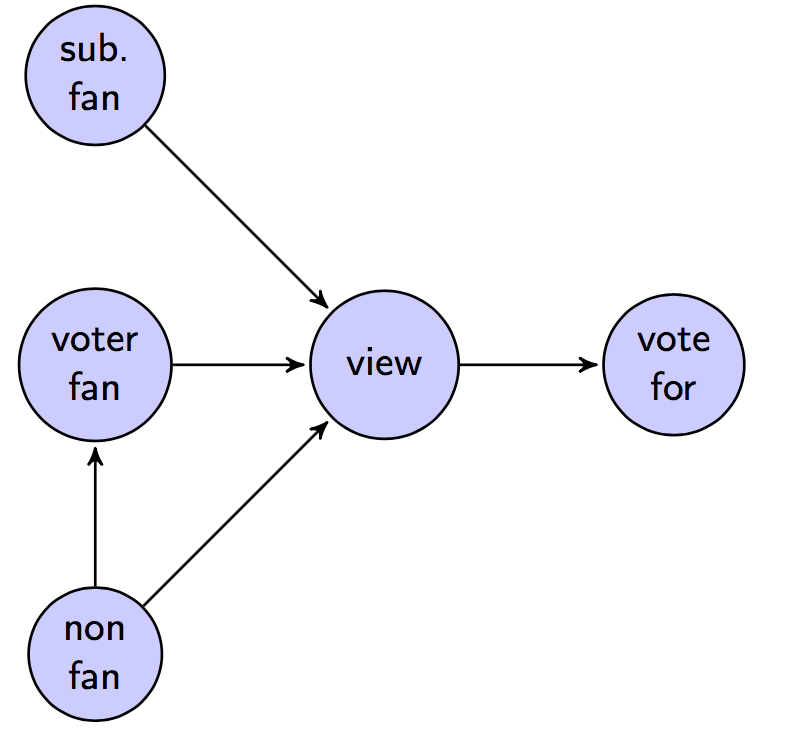
状态转换图假设了用户给查看文章投票的概率与用户如何查看故事是没有关系的：

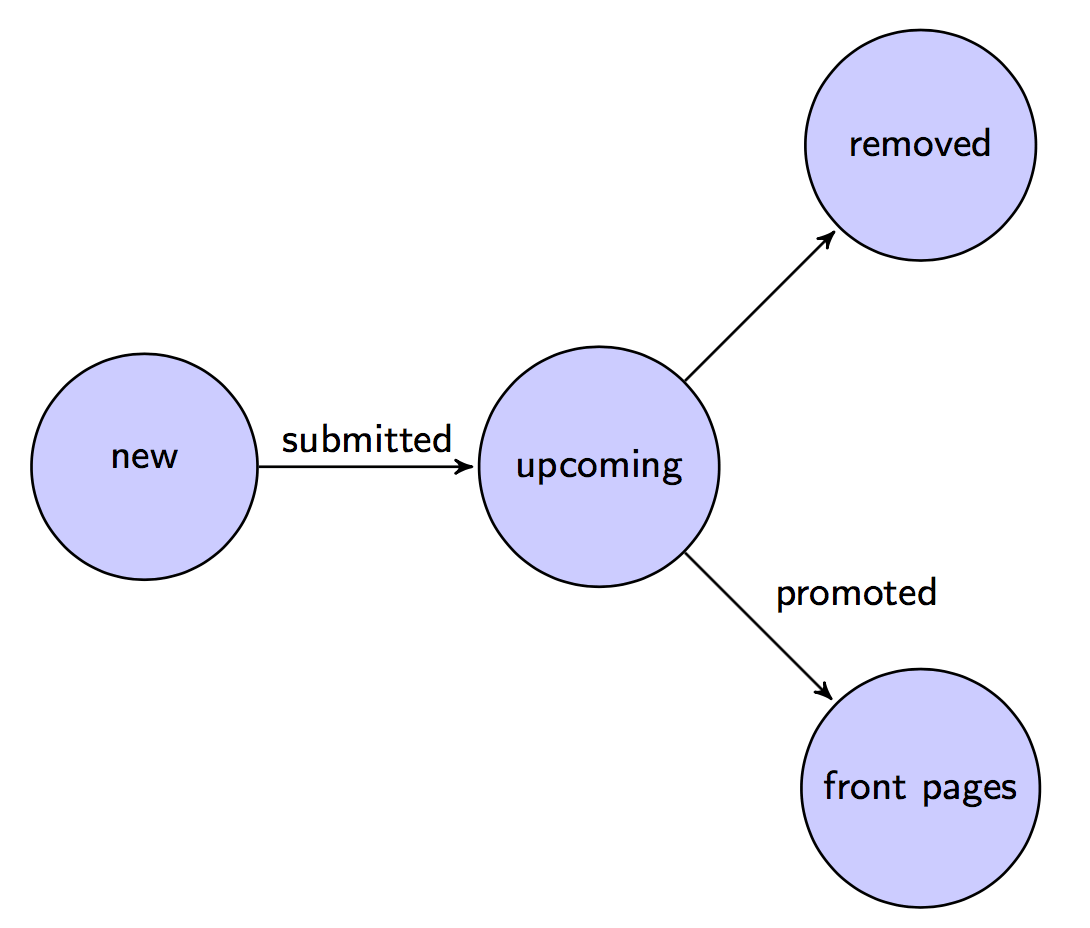
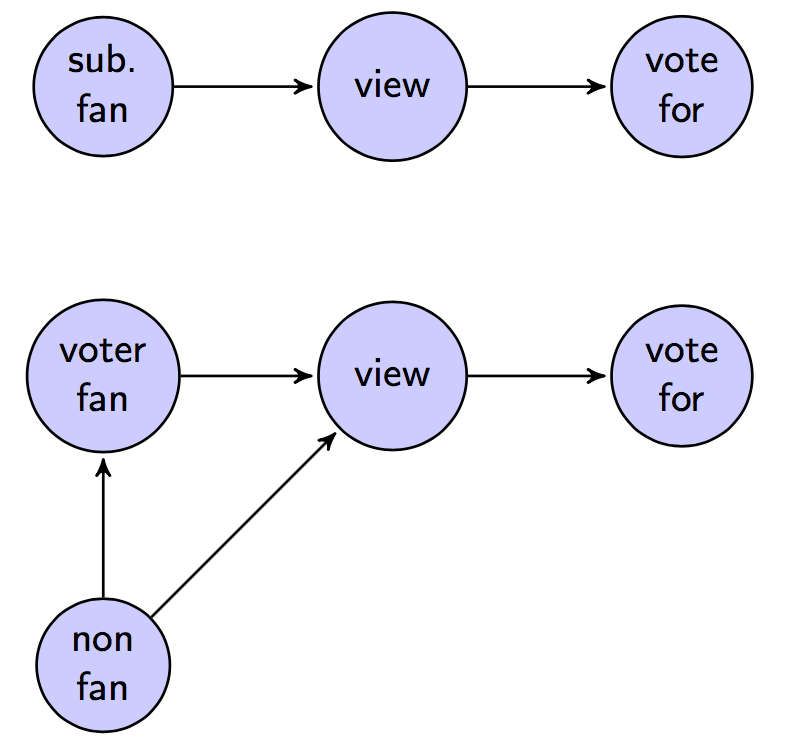
以下状态转换图使得用户查看故事投票的可能性取决于她是否是文章提交者的粉丝：

当模型建立后，每个文章都有两个特征：

其提交者的粉丝数量
查看文章的用户投票的概率（取决于用户是否为提交者的粉丝、投票者的粉丝或非粉丝）。

对于文章的这两个特征的每一对值，表达用户行为的状态转换图的转换被分配概率（基于 Digg 上的频率）。这产生了表达提交给 Digg 的文章的命运的状态转换图的转换的概率。

研究表明，下面两个值是相等的：

表示提交给 Digg 的文章的命运的状态转换图的转换求出的概率
在 Digg 上观察到的相应频率。

这个一致性表明随机模型中考虑的特征解释了 Digg 上的文章的推广行为。

总的来说，随机模型已被用于：

从其流行度的演变（在 Digg 上观察）估计文章的质量（对于 Digg 社区）
从用户对故事的早期反应中预测故事的流行度。

随机建模是一种简单的方法，可以完全依靠社交媒体的信息进行预测。关于更多 Digg 的细节可以参考文献 ⁴。

社会同步性

人类中的社会同步性（social synchrony）的例子有：

在剧院或音乐厅的共同赞美
在整个体育场馆的气氛起伏
舆论的形成
合唱团唱歌
泡沫期间股票交易商的股票行为
开源软件社区的软件开发过程

与社会同步性相关的问题仍在持续研究中，下面有几个关键性的问题：

如何衡量与建模「社会同步」
社会网络结构对「社会同步」的影响是什么？
「社会同步」在何时产生并协同作用？
为什么「社会协同作用」（social synergy）对个人有利？

社会同步的建模

接下来我们来尝试对社会同步这个概念进行建模。首先，描述社交网络的动力学（dynamics）模型可以如下表示：

动力（dynamics）由表示执行某些动作的强度的数值表示
参数：
- $t$：时间
- $i$：个体 ($i=1, …, n$)
- $\pi_i$：i$ 的邻居集
- $s(i, t)$：$i$ 在时刻 $t$ 的状态
- $D(i, t)$：$i$ 在时刻 $t$ 的动力
- $C(i, j, t)$ ：耦合函数，影响时刻 $t$ 时 $j$ 对 $i$ 的影响
- $\delta$：耦合力度
个体 $i$ 在时刻 $t$ 的状态为:

$$ s(i, t) = D(i, t) + \delta \sum_{j\in\pi_i}{C(i,j,t)} $$

如果：

$$ \lim_{t\rightarrow + \infty} {\sum_{i,j}{s(i, t) - s(j, t) = 0}} $$

那么，一组个体 $i = 1, …, n$ 的群体被称为「同步的」（synchronized）。这个方程表示了独立个体的状态会随时间收敛到了一个公共值。

不难发现，这个「社会同步」的定义有两个缺点：

在有限的时间里，为了定义社会同步发生与否，需要考虑无限的时间；
独立个体经常不会在同一时间采取行动。

现考虑独立个体：

独立个体能够处于两个状态（如奶牛躺着或吃饭）
所有状态切换相同次数 $K$
所有状态不一定在同一时间切换

$i$ 和 $j$ 的成对同步（pairwise synchrony）可以定义为： $$ \Delta (i, j) = \frac{1}{K} \sum_{k=1}^{K} |\tau (i, k) - \tau (j, k)| $$

其中 $\tau (i, k)$ 表示 i 在切换第 $k$ 次状态后的时间。于是社会同步可以定义为下面的成对同步的算术平均值：

$$ \Delta = \frac{1}{n^2} \sum_{i,j} \Delta (i, j) $$

现考虑可能处于多个状态的独立个体。在一段时间内的社会同步可以作为次数或者持续时间进行测量，所有或几乎所有的个人处于相同的状态。考虑独立个体及其行动使得：

不同的个体可能在任何时间段以非常不同的速率被激活
一个动作可能持续很短的时间，甚至是瞬间的（也就是没有持续时间）。

其中：

从活动时间序列中，可以使用（一维）聚类算法识别每个独立人活动的突发；
（使用高斯核来）平滑活动突发；
测量成对同步作为两个人的平滑活动突发的相关性；
测量社会同步作为成对同步的平均值；
使用随机模型（或空模型）来检查所测量的社会同步是否显着。

网络结构的影响

现在我们来看看社会网络结构对社会同步的影响。下面的等式给出了一个独立个体的状态：

$$ s(i, t) = D(i, t) + \delta\sum_{i\in\pi_i}{C(i, j, t)} $$

并通过耦合函数 $C$ 使社会同步取决于社会网络结构。

假设：每个人都渴望永远在相邻节点，则耦合函数 $C$ 可以被定义为：

$$ C(i,j,t) = |O(j, t) - O(i, t)| $$ 其中 $O$ 是一个输出函数（output function），表示了个体在他们状态中的改变行为。

独立个体的状态的方程给出了个体 $i$ 在时刻 $t$ 时的状态会变为：

$$ s(i, t) = D(i, t) + \delta\sum_{j\in\pi_i}{L_{ij}O(j, t))} $$

其中 $L=(L_{ij})$ 是社交网络的 Laplacian 矩阵，即当 $i$ 是 $j$ 的邻居时，矩阵的元素的值为 $-1$，如果 $i$ 的度为 $d_i$ 则矩阵元素的值为 $d_i$，否则为 0。

如果网络连接的，则拉普拉斯矩阵的特征值 $\lambda_i$ 满足： $$ \lambda_1= 0 < \lambda_2 \leq … \leq \lambda_n $$ 研究者观察到同步能力（ability to synchronize）的以下特征：

与 $\frac{\lambda_n}{\lambda_2}$成反比（比例越小，同步能力越大）
主要取决于网络的
- 小世界属性（small world property），即两个随机个体之间的最大距离
- 同质性（homogeneity），即个体的社会状态的相似性，即网络中的度。

因此，在全连接网络中，同步的能力是最大的，其中 $\lambda_2=\lambda_n$。

注意：全连接的网络在大型社会中是不现实的。

对社会同步最佳的现实社会网络具有高度均匀的结构，下面这些特征的差异很小：

节点度
两个节点之间的距离
节点中心性，即从任何顶点到通过所考虑节点的任何其他顶点的最短路径数
循环分布

许多现实的社交网络具有模块化的结构（modular structure），也就是拥有社区。研究人员发现两者具有：

中枢节点（高度连接的很多个体）
连接不同模块（社区）的链接

这两个特点在在社会同步中是重要的，是因为：

当中枢节点不受其他人的影响（作为领导者）时，社会同步发生的可能性更大
如果由中枢节点初始化，则更可能出现大规模社会同步
模块之间出现社交同步，但如果模块间链路足够多，则不同的模块才能进行同步

社会同步的优势与增效

总的来说，社会同步促进了协同效应，即「总体优于其部分总和」，并有以下发现：

人际间的同步增加了与群体的联系
社会同步是通过进化来选择的
社会同步有利于集体智慧(collective intelligence)，即社会同步
- 不同任务的群体表现显着正相关
- 然而个体的平均和最高表现没有显着正相关

关于社会同步相关讨论可以进一步阅读这篇文章⁵。

进一步阅读的参考文献

E. Bonabeau: “Agent-Based Modeling: Methods and Techniques for Simulating Human Systems”, Proc. National Academy of Sciences, 99 (Suppl. 3), pp. 7280–7287, 2002 ↩︎
Charles M. Macal and Michael J. North: “ Tutorial on Agent-Based Modeling and Simulation”, Journal of Simulation, 4, pp. 151–162, 2010 ↩︎
Wikipedia: “Comparison of Agent-Based Modeling Software”, http://en.wikipedia.org/wiki/Comparison_of_ agent-based_modeling_software, accessed on 2 May 2014 ↩︎
T. Hogg: “Stochastic Modeling of Social Behavior on Digg”, Handbook of Human Computation, pp. 769-778, 2013 ↩︎
Qi Xuan and Vladimir Filkov: “Synchrony in Social Groups and Its Benefits”, Handbook of Human Computation, pp. 790–802, Springer, 2013 ↩︎