条件收敛和一致收敛
无穷级数理论作为一种工具很有它发明(我们不去讨论它到底是发明还是发现)的必要性。 而一致收敛的引入在现在的数学分析教材上已经变得彻底避而不谈。我们先来讨论一下条件收敛引入的必要性。
我们先来看一个例子,我们知道:
$$ f(n) = 1 - \frac{1}{2} + \frac{1}{3} - \cdots + \left( -1 \right)^{n+1}\frac{1}{n} + \cdots = \ln 2 $$
我们把左边的式子做一些小小的变动,我们把交换一些项的顺序那么:
$$ \begin{split} f(n) &= 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} \cdots + \left( -1 \right)^{n+1}\frac{1}{n} + \cdots \ &= \left( 1 - \frac{1}{2} \right) - \frac{1}{4} + \left( \frac{1}{3} - \frac{1}{6} \right) - \frac{1}{8} + \left( \frac{1}{5} - \frac{1}{10} \right) - \frac{1}{12} + \cdots \ &= \frac{1}{2} - \frac{1}{4} + \frac{1}{6} - \frac{1}{8} + \cdots \ &= \frac{1}{2} f(n) \ &= \frac{1}{2} \ln 2 \end{split} $$
这样荒谬的结论是怎么产生的呢?事实上早在欧拉那个年代,欧拉就为这个问题苦恼并不得其解。直到后来人们才认识到,收敛并不都是相同的,有的具有”很强“的收敛,有的收敛相比之下就显得”较弱“。所以人们就引入了绝对收敛和条件收敛的概念:
定义: 若级数 $\sum^{\infty}{n=1}u{n}$各项的绝对值所构成的正项级数 $\sum^{\infty}{n=1}|u{n}|$收敛,则称级数$\sum^{\infty}{n=1}u{n}$绝对收敛; 如果级数$\sum^{\infty}{n=1}u{n}$收敛,而级数$\sum^{\infty}{n=1}|u{n}|$发散,则称级数$\sum^{\infty}{n=1}u{n}$条件收敛。
并且有下面的定理:
定理: 绝对收敛级数经改变项的位置后构成的级数也收敛,且与原级数有相同的和(即绝对收敛级数具有可交换性)。 如此一来,上面的例子就很好解释了,显然$\sum^{\infty}_{n=1}(-1)^{n-1}\frac{1}{n}$仅仅只是条件收敛,不具备绝对收敛级数的性质。
好的,我们再来讨论一致收敛。
一致收敛为何显得重要,完全得益于下面的这三条性质:
**性质1:**幂级数$\sum^{\infty}{n=0}a{n}x^{n}$的和函数$s(x)$在其收敛域$I$上连续。 **性质2:**幂级数$\sum^{\infty}{n=0}a{n}x^{n}$的和函数$s(x)$在其收敛域$I$上可积,并可逐项积分。 **性质3:**幂级数$\sum^{\infty}{n=0}a{n}x^{n}$在其收敛区间$(-R,R)$内可导,且可逐项求导。
【本节未完】
处处连续却处处不可导的函数
今天想继续写的时候发现电脑里的表达式已经遗失、以后再抽空重新构造吧、、
短期内不想再这上面花时间了、、
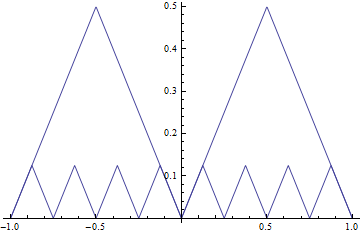
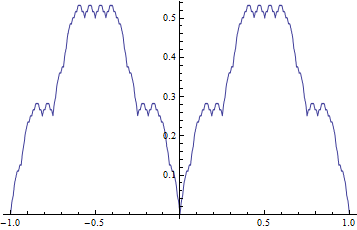
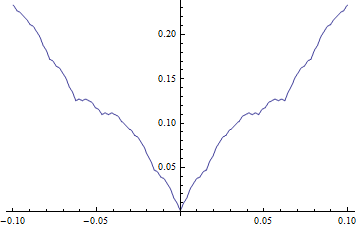
【本节仅存的一些内容】
填满二维区域的一维曲线
【本节未开始】
本文核心内容本来是在5月份就构思完成了,6月1号正式开始着手写这篇博文,但是种种原因拖到现在,但是现在短期内事务较多,加之第二篇中构造的函数已经遗失,不会考虑短期内继续写这篇了。
本文的思路是:通过条件收敛和一致收敛来阐述收敛的意义,以及收敛定义的改写。通过处处连续但处处不可导的函数和填满二位区域的一维曲线来阐述收敛会使函数扩张,并引出某些推广性的结论。