在上一篇文章中，我们讨论了人肉计算领域的意图博弈 GWAPs，通过引入人与人之间游戏博弈的方式来解决计算机难以完成的任务，那么一个绕不开的话题就是应该如何将意图博弈的结果给聚合起来。这也就是本节我们要进一步讨论的内容。

在上一篇文章中我们已经介绍了人肉计算的定义。这篇文章我们来谈谈人肉计算中的「意图博弈」（Game With A Purpose, GWAPs）。

所谓「意图博弈」，指让玩家进行互相博弈，并从博弈过程中收集数据，并用于某种意图。

ESP 游戏

为了说明意图博弈，我们以图像标注这个问题来作为例子。

这篇文章我们来聊聊几个学术界很时髦的几个概念：

• Crowdsourcing (众包)
• Human Computation (人肉计算)
• Wisdom of crowds (群众智慧)

首先，解释一下我将 「Human Computation」译为「人肉计算」的原因：

• 「Human Computation」这一词在中文界尚无公认的标准议法；
• 主流译法为「人计算」、「人本计算」、「人类计算」均欠妥，「人计算」没有译出人为核心的概念，「人本计算」多用于「Human-Centred Computation」，强调以人为本的想法，并未实际替代计算，而「人类计算」则显得概念过于庞大，一个「Human Computation」的系统通常没有涉及「人类」如此之大的范畴。

其次，我们将在下面的内容详细阐述为什么「人肉计算」应当受到重视。

前段时间收到过来自本科母校的对于高年级学长的几个问题，个人感觉问得挺好。这里放出来：

1. 对于一个计科的大学生来说毕业时应具备哪些专业技能，达到一个怎样的水平？

   计算机专业的本科毕业生，我认为应当已经具备极强的学习和工程实践能力。举两个方面为例：

虽然说上次来这边交换的时候也完整体验过门诊的检查体验。但由于没有住过院，并不能算是一段完整的经历。最近「有幸」能够获得一次在德国进行完整住院经历，这次也算是丰富了我在德国的个人体验。

虽然这篇文章的 ID 是 108，但这篇文章已经绝对不是这个博客的第 108 篇文章了。在我本地的文件夹里躺着数十篇尚未写完，也不太想继续写的一些没有价值的内容。

我们都有阅读技术类文章的经历，通常我们为了解决某个问题，在搜索引擎上找到一篇文章，然后随着作者的思路向下阅读，有时候甚至为了能够迅速解决自己的问题直接扫读全文，在不到一分钟的时间里决定这篇文章是否对自己有价值，否则就直接关闭这篇文章。如果凑巧这篇文章对读者有价值，那么这篇文章可能会被引用、会被抄袭，进而广泛传播，对技术圈产生一定的贡献。

然而这一切都是美好的。最初我大学一年级的时候建立这个博客的目的是能够长期写一写自己在技术层面上的积累和感悟。但这几年下来，我发现这件事器其实是一件异常困难的事情。每每当我在电脑里敲下 hexo new "谈某某某技术及xxx" 的命令后，提笔不到半个小时便会被其他事情所吸引，此后便停笔不再续写下去了。

所以你能看到我的博客标签云里「随笔」和「人生感悟」这两个标签的文章比例其实是比较大的。因为这类文章通常不需要进行多少头脑上的思考，只需想到什么就说什么，没什么顾忌，不需要考虑他人的感受。

一篇技术文的生与死

以我个人举例。技术文的动机很明确，记录一下自己近期对于某项技术的心得，当然也包括希望这篇文章能够对他人产生一些帮助。在写一篇技术文之前，我通常会对该项技术进行一个透彻的总览，评估自己对这个技术的理解透彻度，然后确保自己不会犯一些原则性的错误之后开始执笔。

一篇文章的诞生之于我而言，永远不会是线性的产出，我会首先写下一篇文章的整体骨架，然后在之后的成文过程中随时切换到不同的小节中写下自己的思绪，然后在慢慢整理成一篇完整的文章。这差不多算是一篇文章的「生」了。

那么一篇文章的「死」又是怎么回事呢？

因对 Python 感兴趣，于是早上吃早饭时看看。题目相对比较简单，最后一题代码写得比较随意。原本打算交上去测试一下，可惜海外党使用环境实在是卡得惨不忍睹，没办法写敲那么多代码上去。

题目：https://www.shiyanlou.com/contests/lou3/challenges

思维导图

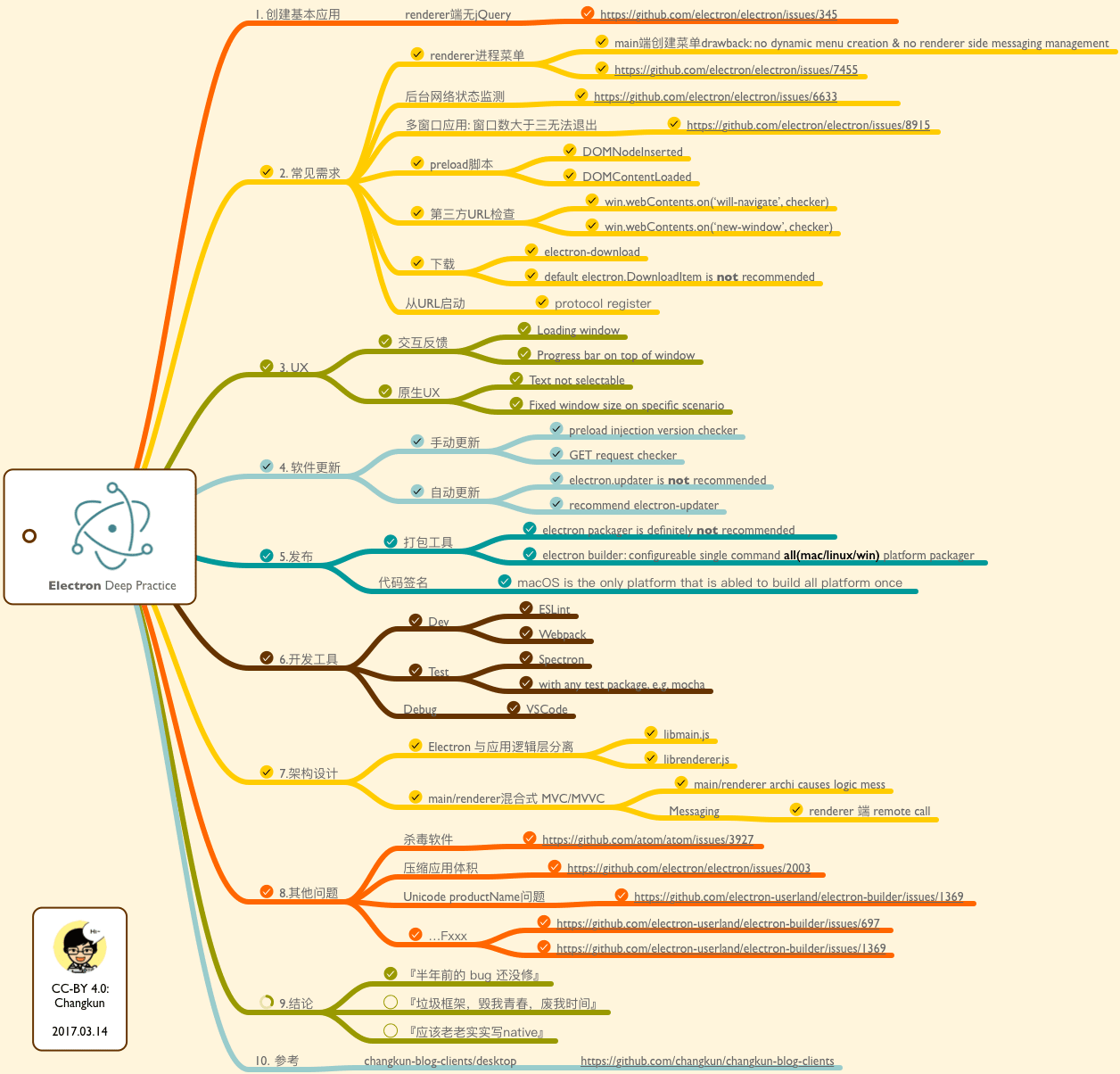
前言:

Electron 从最初发布到现在已经维护很长一段时间了，但是去年才开始慢慢升温。笔者个人恰好也有一些 Electron 的实践经验，原本这篇总结是大约半年前开始起草的，但是由于一些个人原因拖到现在才算是正式完稿，现在发出来供有意实践 Electron 的开发者借鉴，避免一些本人在实践中踩过的坑。此外，笔者的水平有限，难免出现错误，如果读者在阅读本文过程中发现原则性的错误，请务必指出，以免相关内容祸害他人。

本文的实践基于 Electron 1.x 。

创建基本应用

问题: renderer 端无 jQuery

根据官方的新手教程，我们很容易创建一个基本的 Electron 应用，我们不再累赘叙述，如果你只需要加载一个网页，那么只需要下面几行简单的代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

const { BrowserWindow } = require('electron')
let window
function createWindow() {
	window = BrowserWindow({
		width: 1024,
		height 720
	})
	window.loadURL('https://changkun.us')
}
app.on('ready', createWindow)

如果你真的尝试加载笔者的博客页面，会发现笔者博客的文字内容无法加载，这是由于 jQuery 找不到而产生的问题，为此我们并没有必要调整 Web 端的内容，只需要简单在 Electron 的 Renderer 端引入 jQuery 即可。

解决方法就可以使用 BrowserWindow 的 preload 参数，然后使用 preload 脚本为 renderer 端引入 jQuery:

1
2
3
4
5
6

// preload script
document.addEventListener('DOMNodeInserted', (event) => {
  if (!!window && !(window.$)) {
    window.$ = window.jQuery = require('../utils/jquery.min')
  }
})

相关 issue: https://github.com/electron/electron/issues/345